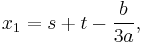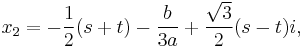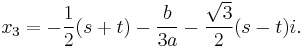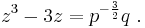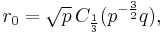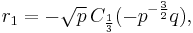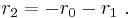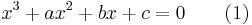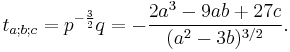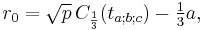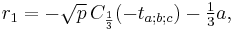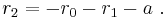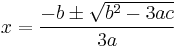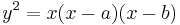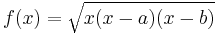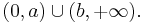Cubic function
- This article discusses cubic equations in one variable. For a discussion of cubic equations in two variables, see elliptic curve.

In mathematics, a cubic function is a function of the form
where a is nonzero; or in other words, a polynomial of degree three. The derivative of a cubic function is a quadratic function. The integral of a cubic function is a quartic function.
Setting ƒ(x) = 0 and assuming a ≠ 0 produces a cubic equation of the form:
Usually, the coefficients a, b,c, d are real numbers. However, most of the theory is also valid if they belong to a field of characteristic other than 2 or 3.
Solving a cubic equation amounts to finding the roots of a cubic function.
Contents
|
History
Cubic equations were known to the ancient Indians and ancient Greeks since the 5th century BC, and even earlier to the ancient Babylonians who were able to solve certain cubic equations, and also to the ancient Egyptians. Doubling the cube is the simplest and oldest studied cubic equation, and one which the ancient Egyptians considered to be impossible.[1] Hippocrates reduced this problem to that of finding two mean proportionals between one line and another of twice its length, but could not solve this with a compass and straightedge construction,[2] a task which is now known to be impossible. Hippocrates, Menaechmus and Archimedes are believed to have come close to solving the problem of doubling the cube using intersecting conic sections,[2] though historians such as Reviel Netz dispute whether the Greeks were thinking about cubic equations or just problems that can lead to cubic equations. Some others like T. L. Heath , who translated all Archimedes' works, disagree, putting forward evidence that Archimedes really solved cubic equations using intersections of two cones, but also discussed the conditions where the roots are 0, 1 or 2.[3]

In the 11th century, the Persian poet-mathematician, Omar Khayyám (1048–1131), made significant progress in the theory of cubic equations. In an early paper he wrote regarding cubic equations, he discovered that a cubic equation can have more than one solution and stated that it cannot be solved using compass and straightedge constructions. He also found a geometric solution which could be used to get a numerical answer by consulting trigonometric tables. In his later work, the Treatise on Demonstration of Problems of Algebra, he wrote a complete classification of cubic equations with general geometric solutions found by means of intersecting conic sections.[4][5]
In the 12th century, another Persian mathematician, [[ ]] (1135–1213), wrote the Al-Mu'adalat (Treatise on Equations), which dealt with eight types of cubic equations with positive solutions and five types of cubic equations which may not have positive solutions. He used what would later be known as the "Ruffini-Horner method" to numerically approximate the root of a cubic equation. He also developed the concepts of a derivative function and the maxima and minima of curves in order to solve cubic equations which may not have positive solutions.[6] He understood the importance of the discriminant of the cubic equation to find algebraic solutions to certain types of cubic equations.[7]
Leonardo de Pisa, also known as Fibonacci (1170–1250), was able to find the positive solution to the cubic equation x3+2x2+10x = 20, using the babylonian numerals. He gave the result as 1,22,7,42,33,4,40 which is equivalent to: 1+22/60+7/602+42/603+33/604+4/605+40/606.[8]
In the early 16th century, the Italian mathematician Scipione del Ferro (1465–1526) found a method for solving a class of cubic equations, namely those of the form x3 + mx = n. In fact, all cubic equations can be reduced to this form if we allow m and n to be negative, but negative numbers were not known to him at that time. Del Ferro kept his achievement secret until just before his death, when he told his student Antonio Fiore about it.
In 1530, Niccolò Tartaglia (1500–1557) received two problems in cubic equations from Zuanne da Coi and announced that he could solve them. He was soon challenged by Fiore, which led to a famous contest between the two. Each contestant had to put up a certain amount of money and to propose a number of problems for his rival to solve. Whoever solved more problems within 30 days would get all the money. Tartaglia received questions in the form x3 + mx = n, for which he had worked out a general method. Fiore received questions in the form x3 + mx2 = n, which proved to be too difficult for him to solve, and Tartaglia won the contest.
Later, Tartaglia was persuaded by Gerolamo Cardano (1501–1576) to reveal his secret for solving cubic equations. In 1539, Tartaglia did so only on the condition that Cardano would never reveal it and that if he did reveal a book about cubics, that he would give Tartaglia time to publish. Some years later, Cardano learned about Ferro's prior work and published Ferro's method in his book Ars Magna in 1545, meaning Cardano gave Tartaglia 6 years to publish his results (with credit given to Tartaglia for an independent solution). Cardano's promise with Tartaglia stated that he not publish Tartaglia's work, and Cardano felt he was publishing del Ferro's, so as to get around the promise. Nevertheless, this led to a challenge to Cardano by Tartaglia, which Cardano denied. The challenge was eventually accepted by Cardano's student Lodovico Ferrari (1522–1565). Ferrari did better than Tartaglia in the competition, and Tartaglia lost both his prestige and income [9].
Cardano noticed that Tartaglia's method sometimes required him to extract the square root of a negative number. He even included a calculation with these complex numbers in Ars Magna, but he did not really understand it. Rafael Bombelli studied this issue in detail and is therefore often considered as the discoverer of complex numbers.
Roots of a cubic function
The nature of the roots
Every cubic equation with real coefficients has at least one solution x among the real numbers; this is a consequence of the intermediate value theorem. We can distinguish several possible cases using the discriminant,
The following cases need to be considered: [10]
- If Δ > 0, then the equation has three distinct real roots.
- If Δ = 0, then the equation has a multiple root and all its roots are real.
- If Δ < 0, then the equation has one real root and two nonreal complex conjugate roots.
See also: multiplicity of a root of a polynomial
General formula of roots
For the general cubic equation 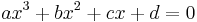 , if
, if 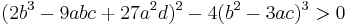 , the general formulas for the roots, in terms of the coefficients, are as follows:[11]
, the general formulas for the roots, in terms of the coefficients, are as follows:[11]
However this formula is wrong if the operand of the square root is negative: When it is positive, the cubic roots are real and well defined. On the other hand, if the operand of the square root is negative, the square root is not real and one has to choose, once for all a determination for it, for example the one with positive imaginary part. For extracting the cubic roots we have also to choose a determination for the cubic roots, and this gives nine possible values for the first root of an equation which has only three roots.
A correct solution may be obtained by remarking that the proof of above formula shows that the product of the two cubic roots is rational. This gives the following formula in which 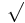 or
or ![\sqrt[3]{ }](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/9bbd095bafd3ae229d6baa25f34ebe84.png) stand for any determination of the square or cubic root.
stand for any determination of the square or cubic root.
Monic formula of roots
For a monic polynomial (dividing by the leading coefficient), renaming the coefficients as 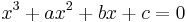 , this reduces to
, this reduces to
Introducing the following notation
simplifies the above equations to
In this form, they can be identified as the inverse discrete Fourier transform of the triple:
which is the perspective taken in the method of Lagrange resolvents.
Since there are 3 possible values for each cube root, ![\alpha = \sqrt[3]{\frac{m+\sqrt{n}}{2}}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/bf79e5df5b56ef7ff9edd122480bb102.png) and
and ![\beta = \sqrt[3]{\frac{m-\sqrt{n}}{2}}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/bb87ac32268eb95c206a9336e3213b47.png) must be taken so that they satisfy
must be taken so that they satisfy 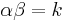 .
.
Cardano's method
The solutions can be found with the following method due to Scipione del Ferro and Tartaglia, published by Gerolamo Cardano in 1545.[12]
We first divide the standard equation by the leading coefficient to arrive at an equation of the form
The substitution 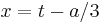 eliminates the quadratic term, giving the so-called depressed cubic
eliminates the quadratic term, giving the so-called depressed cubic
where
We introduce two variables u and v linked by the condition
and substitute this in the depressed cubic (2), giving
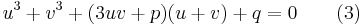 .
.
At this point Cardano imposed a second condition for the variables u and v
which, combined with (3) (the first parenthesis vanishes, then multiply by u3 and substitute uv) gives
This can be seen as a quadratic equation in u3. When we solve this equation, we find that
and thus
Since t = v + u, t = x + a/3, and v = −p/3u, we find
Note that there are six possibilities in computing u with (4), since there are two possibilities for the square root (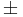 ), and three for the cubic root (the principal root and the principal root multiplied by
), and three for the cubic root (the principal root and the principal root multiplied by 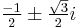 ). The sign of the square root however does not affect the resulting t (a simple calculation shows that −p/3u = v), although care must be taken in three special cases to avoid divisions by zero:
). The sign of the square root however does not affect the resulting t (a simple calculation shows that −p/3u = v), although care must be taken in three special cases to avoid divisions by zero:
- First, if p = q = 0, then we have the triple real root
- Second, if p = 0 and q ≠ 0, then
- Third, if p ≠ 0 and q = 0 then
- in which case the three roots are
- where
Summary
In summary, for the cubic equation
the solutions for x are given by
where
The expression above for u can generate up to three values (there are three cubic roots related by a factor which is one of the two non-real cubic roots of one, and two square roots of any sign ; but these 6 expressions can generate only 3 pairs). This also applies to the final solutions for x.
Alternative method
An alternative method to obtain the same results is as follows.
We know that
Since u and v must satisfy
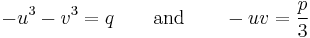 ,
,
it can be shown that
Writing out the three cube roots we get
Remembering t = u + v we get only three possible values for t because only three combinations of u and v are possible if 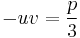 is to remain valid as it must — so
is to remain valid as it must — so
and x is obtained from
The above methods do apply if p and q are complex. This solution avoids the addition of an inverted cubic radical in the solution, and also resolves the ambiguity of signs for the square roots in the first solution given above.
- Summary
To simplify the expressions above, it is customary to define this resolution in several steps by defining intermediate variables. Let
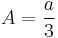 and
and 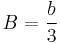
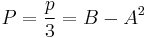
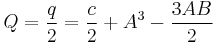
Then the discriminant of the quadratic equation of 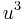 or
or 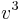 is
is
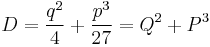 ,
,
Let's also define a constant that represents a generator for the three cubic roots of unity:
Then the solutions for x = t - A can be simply defined for k in 0, 1, 2 in :
where 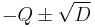 are the two possible values for
are the two possible values for 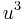 or
or 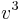 .
.
In the case p and q are both real, the following cases can be distinguished, according to the sign of the discriminant.
- If D is strictly positive then there are one real root and two non-real, conjugate roots.
- If D is zero then there is one real root (a triple root) or two real roots (a single root and a double root).
- If D is strictly negative then there are three real roots. (In this case, if the cubic function has real coefficients but its real roots cannot be expressed with real radicals, then this is the casus irreducibilis).
Lagrange resolvents
Description
Lagrange resolvents, introduced by Joseph Louis Lagrange in his paper Réflexions sur la résolution algébrique des équations, reduced the solution of a cubic equation to the solution of an auxiliary quadratic polynomial, the "resolving equation" or resolvent quadratic of the original equation,[13][14] by a change of variables from the roots 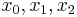 to the Lagrange resolvents
to the Lagrange resolvents 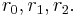 In modern terms, the resolvents are the discrete Fourier transform of the original roots.
In modern terms, the resolvents are the discrete Fourier transform of the original roots.
In the modern language of Galois theory, Lagrange exploited the fact that the symmetric group S3 has the cyclic group of order three 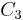 as a normal subgroup, thus allowing one to decompose the permutation group of the roots as
as a normal subgroup, thus allowing one to decompose the permutation group of the roots as 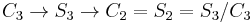 – the
– the 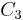 corresponds to the discrete Fourier transform (of order 3), while the
corresponds to the discrete Fourier transform (of order 3), while the 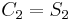 corresponds to the quadratic resolving polynomial.
corresponds to the quadratic resolving polynomial.
In the same way, the symmetric group of order four S4 has a Klein four-group as normal subgroup, with quotient a symmetric group of order three S3, which allows one to solve a quartic in terms of a cubic resolving polynomial.
However, this method does not work for polynomials of degree five or greater, as the resolving polynomial has higher degree than the original polynomial (for a quintic the resolving polynomial has degree 24[13]). This is explained by the Abel–Ruffini theorem, which proves that such polynomials cannot be solved by radicals.
Procedure
Suppose that r0, r1 and r2 are the roots of equation (1), and define 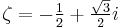 , so that ζ is a primitive third root of unity. We now set
, so that ζ is a primitive third root of unity. We now set
This is the discrete Fourier transform of the roots: observe that while the coefficients of the polynomial are symmetric in the roots, in this formula an order has been chosen on the roots, so these are not symmetric in the roots. The roots may then be recovered from the three si by inverting the above linear transformation via the inverse discrete Fourier transform, giving
We already know the value s0 = −a, so we only need to seek values for the other two.
The 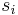 are not symmetric in the roots –
are not symmetric in the roots –  is invariant, while the two non-trivial cyclic permutations of the roots send
is invariant, while the two non-trivial cyclic permutations of the roots send  to
to 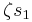 and
and  to
to 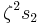 , or
, or  to
to 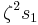 and
and  to
to 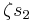 (depending on which permutation), while transposing
(depending on which permutation), while transposing 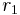 and
and 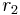 switches
switches  and
and  – other transpositions switch these roots and multiplying them by a power of
– other transpositions switch these roots and multiplying them by a power of 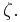
Thus, if one takes the cubes, the factors of  become factors of
become factors of 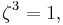 so every cyclic permutation leaves the cubes invariant, and a transposition of two roots exchanges s13 and s23 – in other words,
so every cyclic permutation leaves the cubes invariant, and a transposition of two roots exchanges s13 and s23 – in other words, 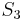 (permutation of the roots) acts as a permutation group on
(permutation of the roots) acts as a permutation group on 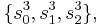 specifically by the sign permutation exchanging the last two, meaning that the action factors through the sign map
specifically by the sign permutation exchanging the last two, meaning that the action factors through the sign map 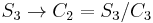 corresponding to the cyclic group of order 3 being a normal subgroup.
corresponding to the cyclic group of order 3 being a normal subgroup.
Hence the polynomial
is invariant under permutations of the roots, and so has coefficients expressible in terms of (1). Using calculations involving symmetric functions or alternatively field extensions, we can calculate (5) to be
The roots of this quadratic equation are
where D is the discriminant. Taking cube roots give us s1 and s2, from which we can recover the roots ri of (1).
Factorization
If r is any root of (1), then we may factor using r to obtain
Hence if we know one root we can find the other two by solving a quadratic equation, giving
for the other two roots.
Root-finding formula
The formula for finding the roots of a cubic function, based on Cardano's method, is fairly complicated. Therefore, it is common to use the rational root test or a numerical solution instead.
If we have
with 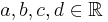 and
and 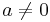 , let
, let
and
we define the discriminant:
There are two distinct cases:
- in which case there are one real root and two non-real roots that are conjugate. We define:
- and
- in which case we have 3 real roots. We express the complex quantity
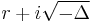 in polar form:
in polar form:
- and we define:
- and
In both cases, the solutions are
Solution in terms of Chebyshev radicals
If we have a cubic equation which is already in depressed form, we may write it as 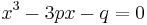 . Substituting
. Substituting 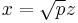 we obtain
we obtain 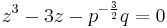 or equivalently
or equivalently
From this we obtain solutions to our original equation in terms of the Chebyshev cube root 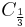 as
as
If now we start from a general equation
and reduce it to the depressed form under the substitution x = t − a/3, we have 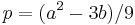 and
and 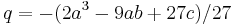 , leading to
, leading to
This gives us the solutions to (1) as
The case of a cubic equation with real coefficients
Suppose the coefficients of (1) are real. If s is the quantity q/r from the section on real roots, then s = t2; hence 0 < s < 4 is equivalent to −2 < t < 2, and in this case we have a polynomial with three distinct real roots, expressed in terms of a real function of a real variable, quite unlike the situation when using cube roots. If s > 4 then either t > 2 and 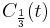 is the sole real root, or t < −2 and
is the sole real root, or t < −2 and 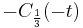 is the sole real root. If s < 0 then the reduction to Chebyshev polynomial form has given a t which is a pure imaginary number; in this case
is the sole real root. If s < 0 then the reduction to Chebyshev polynomial form has given a t which is a pure imaginary number; in this case 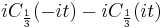 is the sole real root. We are now evaluating a real root by means of a function of a purely imaginary argument; however we can avoid this by using the function
is the sole real root. We are now evaluating a real root by means of a function of a purely imaginary argument; however we can avoid this by using the function
which is a real function of a real variable with no singularities along the real axis. If a polynomial can be reduced to the form 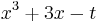 with real t, this is a convenient way to solve for its roots.
with real t, this is a convenient way to solve for its roots.
Derivative
Through the quadratic formula the roots of the derivative
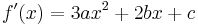 ,
,
are given by
and provide the critical points where the slope of the cubic equation is zero. If b2-3ac>0, then the cubic function has a local maximum and a local minimum. If b2-3ac=0, then the cubic's inflection point is the only critical point. If b2-3ac<0, then there are no critical points. In the cases where b2-3ac≤0, the cubic is strictly monotonic.
Bipartite cubics
The graph of
where 0<a<b , is called a bipartite cubic. This is from the theory of elliptic curves.
One can graph a bipartite cubic on a graphing device by graphing the function
corresponding to the upper half of the bipartite cubic. It is defined on
See also
- Casus irreducibilis
- Linear equation
- Quadratic equation
- Quartic equation
- Quintic equation
- Polynomial
- Newton's method
- Spline (mathematics)
- Viete
Notes
- ↑ Guilbeau (1930, p. 8) states, "The Egyptians considered the solution impossible, but the Greeks came nearer to a solution."
- ↑ 2.0 2.1 Guilbeau (1930, pp. 8–9)
- ↑ The works of Archimedes, translation by T. L. Heath
- ↑ J. J. O'Connor and E. F. Robertson (1999), Omar Khayyam, MacTutor History of Mathematics archive, states, "Khayyam himself seems to have been the first to conceive a general theory of cubic equations."
- ↑ Guilbeau (1930, p. 9) states, "Omar Al Hay of Chorassan, about 1079 AD did most to elevate to a method the solution of the algebraic equations by intersecting conics."
- ↑ O'Connor, John J.; Robertson, Edmund F., "Sharaf al-Din al-Muzaffar al-Tusi", MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Al-Tusi_Sharaf.html.
- ↑ J. L. Berggren (1990), "Innovation and Tradition in Sharaf al-Din al-Tusi's Muadalat", Journal of the American Oriental Society 110 (2): 304–9
- ↑ "The life and numbers of Fibonacci" [1], Plus Magazine
- ↑ Katz, Victor. A History of Mathematics. pp. 220. Boston: Addison Wesley, 2004.
- ↑ Irving, Ronald S. (2004), Integers, polynomials, and rings, Springer-Verlag New York, Inc., ISBN 0-387-40397-3, http://books.google.com/?id=B4k6ltaxm5YC, Chapter 10 ex 10.14.4 and 10.17.4, p. 154-156
- ↑ http://hk.knowledge.yahoo.com/question/question?qid=7007111502216
- ↑ Jacobson (2009), p. 210.
- ↑ 13.0 13.1 Prasolov, Viktor; Solovyev, Yuri (1997), Elliptic functions and elliptic integrals, AMS Bookstore, ISBN 978 0 82180587 9, http://books.google.com/?id=fcp9IiZd3tQC, §6.2, p. 134
- ↑ Kline, Morris (1990), Mathematical Thought from Ancient to Modern Times, Oxford University Press US, ISBN 978 0 19506136 9, http://books.google.com/?id=aO-v3gvY-I8C, Algebra in the Eighteenth Century: The Theory of Equations
References
- Anglin, W. S.; Lambek, Joachim (1995), "Mathematics in the Renaissance", The Heritage of Thales, Springers, pp. 125–131, ISBN 978-0387945446, http://books.google.com/?id=mZfXHRgJpmQC&pg=PA125&lpg=PA125&dq=%22mathematics+in+the+renaissance%22+heritage+thales&q Ch. 24.
- Guilbeau, Lucye (1930), "The History of the Solution of the Cubic Equation", Mathematics News Letter 5 (4): 8–12, doi:10.2307/3027812, http://jstor.org/stable/3027812
- Jacobson, Nathan (2009), Basic algebra, 1 (2nd ed.), Dover, ISBN 978-0-486-47189-1
- Nickalls, R. W. D. (November 1993), "A new approach to solving the cubic: Cardan's solution revealed", The Mathematical Gazette 77 (480): 354–359, doi:10.2307/3619777, ISSN 0025-5572, http://www.nickalls.org/dick/papers/maths/cubic1993.pdf
- Henriquez, G., "The graphical interpretation of the complex roots of cubic equations," American Mathematical Monthly 42, June-July 1935, 383-384.
- Dunnett, R., "Newton-Raphson and the cubic," Mathematical Gazette 78, November 1994, 347-348.
- Dence, T., "Cubics, chaos and Newton's method," Mathematical Gazette 81, November 1997, 403-408.
- Holmes, G. C., "The use of hyperbolic cosines in solving cubic polynomials," Mathematical Gazette 86, Novemebr 2002, 473-477.
- Nickalls, R. W. D., "Viète, Descartes and the cubic equation," Mathematical Gazette 90, July 2006, 203-208.
- Mitchell, D. W., "Solving cubics by solving triangles," Mathematical Gazette 91, November 2007, 514-516.
- Zucker, I. J., "The cubic equation—A new look at the irreducible case," Mathematical Gazette 92, July 2008, 264-268.
- Rechtschaffen, E., "Real roots of cubics: Explicit formula for quasi-solutions," Mathematical Gazette 92, July 2008, 268-276.
- Mitchell, D. W., "Powers of
 as roots of cubics," Mathematical Gazette 93, November 2009.
as roots of cubics," Mathematical Gazette 93, November 2009.
External links
- Solving a Cubic by means of Moebius transforms
- Interesting derivation of trigonometric cubic solution with 3 real roots
- Calculator for solving Cubics (also solves Quartics and Quadratics)
- Tartaglia's work (and poetry) on the solution of the Cubic Equation at Convergence
- Cubic Equation Solver.
- Quadratic, cubic and quartic equations on MacTutor archive.
- Cubic Formula on PlanetMath
- Cardano solution calculator as java applet at some local site. Only takes natural coefficients.
- Graphic explorer for cubic functions With interactive animation, slider controls for coefficients
- On Solution of Cubic Equations at Holistic Numerical Methods Institute
- Dave Auckly, Solving the quartic with a pencil American Math Monthly 114:1 (2007) 29—39
- "Cubic Equation" by Eric W. Weisstein, The Wolfram Demonstrations Project, 2007.
- The affine equivalence of cubic polynomials at Dynamic Geometry Sketches
|
|||||
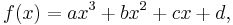
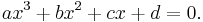
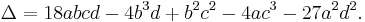
![\begin{align}
x_1 =
&-\frac{b}{3 a}\\
&-\frac{1}{3 a} \sqrt[3]{\tfrac12\left[2 b^3-9 a b c+27 a^2 d+\sqrt{\left(2 b^3-9 a b c+27 a^2 d\right)^2-4 \left(b^2-3 a c\right)^3}\right]}\\
&-\frac{1}{3 a} \sqrt[3]{\tfrac12\left[2 b^3-9 a b c+27 a^2 d-\sqrt{\left(2 b^3-9 a b c+27 a^2 d\right)^2-4 \left(b^2-3 a c\right)^3}\right]}\\
x_2 =
&-\frac{b}{3 a}\\
&+\frac{1+i \sqrt{3}}{6 a} \sqrt[3]{\tfrac12\left[2 b^3-9 a b c+27 a^2 d+\sqrt{\left(2 b^3-9 a b c+27 a^2 d\right)^2-4 \left(b^2-3 a c\right)^3}\right]}\\
&+\frac{1-i \sqrt{3}}{6 a} \sqrt[3]{\tfrac12\left[2 b^3-9 a b c+27 a^2 d-\sqrt{\left(2 b^3-9 a b c+27 a^2 d\right)^2-4 \left(b^2-3 a c\right)^3}\right]}\\
x_3 =
&-\frac{b}{3 a}\\
&+\frac{1-i \sqrt{3}}{6 a} \sqrt[3]{\tfrac12\left[2 b^3-9 a b c+27 a^2 d+\sqrt{\left(2 b^3-9 a b c+27 a^2 d\right)^2-4 \left(b^2-3 a c\right)^3}\right]}\\
&+\frac{1+i \sqrt{3}}{6 a} \sqrt[3]{\tfrac12\left[2 b^3-9 a b c+27 a^2 d-\sqrt{\left(2 b^3-9 a b c+27 a^2 d\right)^2-4 \left(b^2-3 a c\right)^3}\right]}
\end{align}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/7f19af779a9bea4db300039405693001.png)
![\begin{align}
Q = &\sqrt{(2 b^3-9 a b c+27 a^2 d)^2-4 (b^2-3 a c)^3}\\
C = &\sqrt[3]{\tfrac12 (Q + 2 b^3-9 a b c+27 a^2 d)}\\
x_1 = &-\frac{b}{3 a}-\frac{C}{3 a}-\frac{b^2-3 a c}{3 a C}\\
x_2 = &-\frac{b}{3 a}+\frac{C(1+i \sqrt{3})}{6 a} +\frac{(1-i \sqrt{3}) (b^2-3 a c)}{6 a C}\\
x_3 = &-\frac{b}{3 a}+\frac{C(1-i \sqrt{3})}{6 a} +\frac{(1+i \sqrt{3}) (b^2-3 a c)}{6 a C}
\end{align}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/348ffa4b63eb0ddd0c4391c9605e6865.png)
![\begin{align}
x_1 =
&-\frac{a}{3}\\
&-\frac{1}{3} \sqrt[3]{\tfrac12\left[2 a^3-9 a b+27 c+\sqrt{\left(2 a^3-9 a b +27 c\right)^2-4 \left(a^2-3 b\right)^3}\right]}\\
&-\frac{1}{3} \sqrt[3]{\tfrac12\left[2 a^3-9 a b+27 c-\sqrt{\left(2 a^3-9 a b +27 c\right)^2-4 \left(a^2-3 b\right)^3}\right]}\\
x_2 =
&-\frac{a}{3}\\
&+\frac{1+i \sqrt{3}}{6} \sqrt[3]{\tfrac12\left[2 a^3-9 a b+27 c+\sqrt{\left(2 a^3-9 a b +27 c\right)^2-4 \left(a^2-3 b\right)^3}\right]}\\
&+\frac{1-i \sqrt{3}}{6} \sqrt[3]{\tfrac12\left[2 a^3-9 a b+27 c-\sqrt{\left(2 a^3-9 a b +27 c\right)^2-4 \left(a^2-3 b\right)^3}\right]}\\
x_3 =
&-\frac{a}{3}\\
&+\frac{1-i \sqrt{3}}{6} \sqrt[3]{\tfrac12\left[2 a^3-9 a b+27 c+\sqrt{\left(2 a^3-9 a b +27 c\right)^2-4 \left(a^2-3 b\right)^3}\right]}\\
&+\frac{1+i \sqrt{3}}{6} \sqrt[3]{\tfrac12\left[2 a^3-9 a b+27 c-\sqrt{\left(2 a^3-9 a b +27 c\right)^2-4 \left(a^2-3 b\right)^3}\right]}\\
\end{align}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/3e5e5dade261b4f948183de6d8a9b777.png)
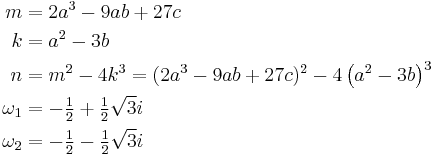
![\begin{align}
x_1 &= -\frac{1}{3}
\left(a
+ \quad \sqrt[3]{\frac{m+\sqrt{n}}{2}}
+ \quad \sqrt[3]{\frac{m-\sqrt{n}}{2}} \,\right)\\
x_2 &= -\frac{1}{3}
\left( a
+\omega_2 \sqrt[3]{\frac{m+\sqrt{n}}{2}}
+\omega_1 \sqrt[3]{\frac{m-\sqrt{n}}{2}} \,\right)\\
x_3 &= -\frac{1}{3}
\left( a
+\omega_1 \sqrt[3]{\frac{m+\sqrt{n}}{2}}
+\omega_2 \sqrt[3]{\frac{m-\sqrt{n}}{2}} \,\right)\\
\end{align}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/0dff7e13699e51076b6581aa6b642147.png)
![\left(
-a, -\sqrt[3]{\frac{m+\sqrt{n}}{2}}, -\sqrt[3]{\frac{m-\sqrt{n}}{2}}
\right)](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/19debaace462151ade46871dc58aacb6.png)
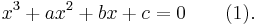
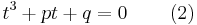
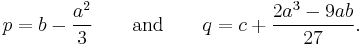
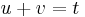
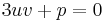
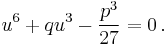
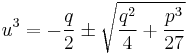
![u=\sqrt[3]{-{q\over 2}\pm \sqrt{{q^{2}\over 4}+{p^{3}\over 27}}} \qquad (4)](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/ca28f56d9a9579116905053774c6f0ee.png)
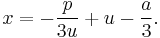
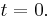
![u=0 \text{ and } v = -\sqrt[3]{q}.](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/35d6f22880e00aec8d0d8c2eb3da1701.png)
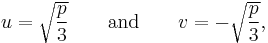
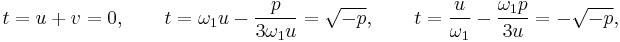
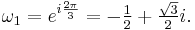
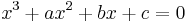
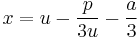
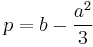
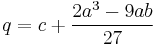
![u = \sqrt[3]{-{q \over 2} \pm \sqrt{{q^2 \over 4} + {p^3 \over 27}}}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/46d52446f1f76ca06bf3b2fa271701a8.png)
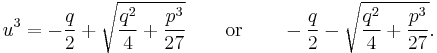

![u=\left\{ \begin{align}
& \sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^{2}}{4}+\frac{p^{3}}{27}}} \\
& \left( -\tfrac{1}{2}+\tfrac{\sqrt{3}}{2}i \right)\sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^{2}}{4}+\frac{p^{3}}{27}}} \\
& \left( -\tfrac{1}{2}-\tfrac{\sqrt{3}}{2}i \right)\sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^{2}}{4}+\frac{p^{3}}{27}}} \\
\end{align} \right.\text{ and }v=\left\{ \begin{align}
& \sqrt[3]{-\frac{q}{2}-\sqrt{\frac{q^{2}}{4}+\frac{p^{3}}{27}}} \\
& \left( -\tfrac{1}{2}+\tfrac{\sqrt{3}}{2}i \right)\sqrt[3]{-\frac{q}{2}-\sqrt{\frac{q^{2}}{4}+\frac{p^{3}}{27}}} \\
& \left( -\tfrac{1}{2}-\tfrac{\sqrt{3}}{2}i \right)\sqrt[3]{-\frac{q}{2}-\sqrt{\frac{q^{2}}{4}+\frac{p^{3}}{27}}} \\
\end{align} \right.](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/97d167cd3871cbe4f3a0148316ee48fd.png)
![t=\left\{ \begin{align}
& \sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^{2}}{4}+\frac{p^{3}}{27}}}+\sqrt[3]{-\frac{q}{2}-\sqrt{\frac{q^{2}}{4}+\frac{p^{3}}{27}}} \\
& \left( -\tfrac{1}{2}+\tfrac{\sqrt{3}}{2}i \right)\sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^{2}}{4}+\frac{p^{3}}{27}}}+\left( -\tfrac{1}{2}-\tfrac{\sqrt{3}}{2}i \right)\sqrt[3]{-\frac{q}{2}-\sqrt{\frac{q^{2}}{4}+\frac{p^{3}}{27}}} \\
& \left( -\tfrac{1}{2}-\tfrac{\sqrt{3}}{2}i \right)\sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^{2}}{4}+\frac{p^{3}}{27}}}+\left( -\tfrac{1}{2}+\tfrac{\sqrt{3}}{2}i \right)\sqrt[3]{-\frac{q}{2}-\sqrt{\frac{q^{2}}{4}+\frac{p^{3}}{27}}} \\
\end{align} \right.](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/ccb9fcc02b85958b7ed8b8d581364989.png)
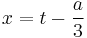
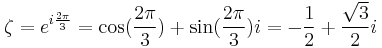
![\begin{align}
x_k & = t_k - A \\
& = \zeta^k . \sqrt[3]{-Q + \sqrt{D}} + \zeta^{2k} . \sqrt[3]{-Q - \sqrt{D}} - A \\
& = -\left( \zeta^k . \sqrt[3]{Q - \sqrt{D}} + \zeta^{2k} . \sqrt[3]{Q + \sqrt{D}} + A \right) \\
\end{align}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/5edc96e87d6e38e2c9eba92634bb6d1d.png)
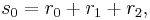
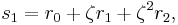
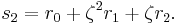
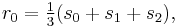
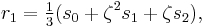
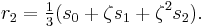
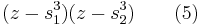
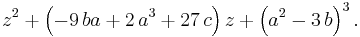
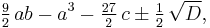
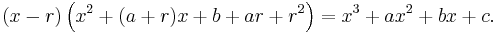
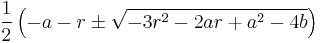
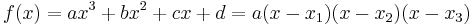
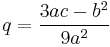
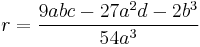
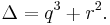
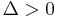
![s = \sqrt[3]{r + \sqrt{q^3+r^2}}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/fff0471efcb5577957aded44687425aa.png)
![t = \sqrt[3]{r - \sqrt{q^3+r^2}}.](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/d1094d689182f9c20ac36f214fc67555.png)
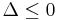
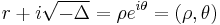
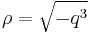
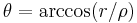
![s = (\sqrt[3]{\rho}, \theta/3).\,](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/5dce044e96b344117ae2662cb5c6ae61.png)
![t = (\sqrt[3]{\rho}, -\theta/3).\,](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/7a180c1881a0b8e87fbbd5ead5b2af5c.png)